The masked normalized cross-correlation and its application to image registration

Image registration consists in determinining the most likely transformation between two images — most importantly translation, which is what I am most concerned with.

How can we detect the translation between two otherwise similar image? This is an application of cross-correlation. The cross-correlation of two images is the degree of similitude between images for every possible translation between them. Mathematically, given grayscale images as discrete functions $I_1(i,j)$ and $I_2(i,j)$, their cross-correlation $I_1 \star I_2$ is defined as: $$(I_1 \star I_2)(u, v) \equiv \sum_{i,j} I_1(i, j) \cdot I_2(i - u, j - v)$$

For example, if $I_1 = I_2$, then $I_1 \star I_2$ has its maximum at $(u,v) =$ (0,0). What happens if $I_1$ and $I_2$ are shifted from each other? Let’s see:

In the above example, the cross-correlation is maximal at (50, 0), which is exactly the translation required to shift back the second image to match the first one. Finding the translation between images is then a simple matter of determining the glocal maximum of the cross-correlation. This operation is so useful that it is implemented in the Python library scikit-image as skimage.feature.phase_cross_correlation.

It turns out that in my field of research, image registration can be crucial to correct experimental data. My primary research tool is ultrafast electron diffraction. Without knowing the details, you can think of this technique as a kind of microscope. A single image from one of our experiments looks like this:

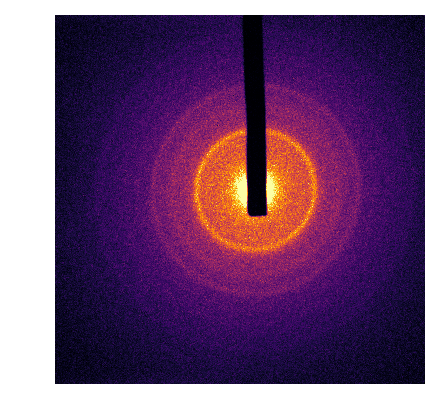
Most of the electron beam is unperturbed by the sample; this is why we use a metal beam-block (seen as a black rod in the image above) to prevent the electrons from damaging our apparatus.

Our experiments are synthesized from hundreds of gigabytes of images like the one above, and it may take up to 72h (!) to take all the images we need. Over the course of this time, the electron beam may shift in a way that moves the image, but not the beam-block¹. Heres’s what I mean:

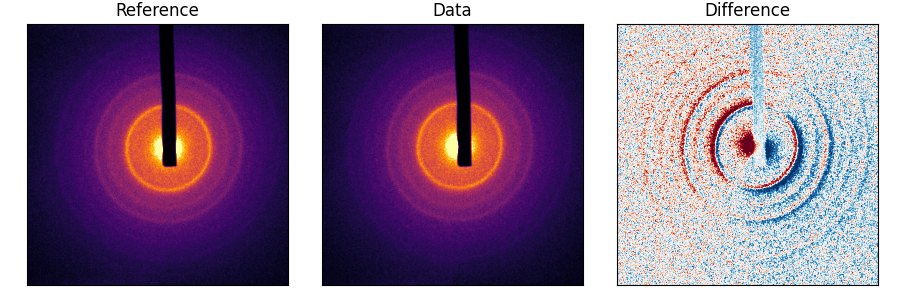
This does not fly. We need to be able to compare images together, and shifts by more than 1px are problematic. We need to correct for this shift, for every image, with respect to the first one. However, we are also in a bind, because unlike the example above, the images are not completely shifted; one part of them, the beam-block, is static, while the image behind it shifts.

The crux of the problem is this: the cross-correlation between images gives us the shift between them. However, it is not immediately obvious how to tell the cross-correlation operation to ignore certain parts of the image. Is there some kind of operation, similar to the cross-correlation, that allows to mask parts of the images we want to ignore?

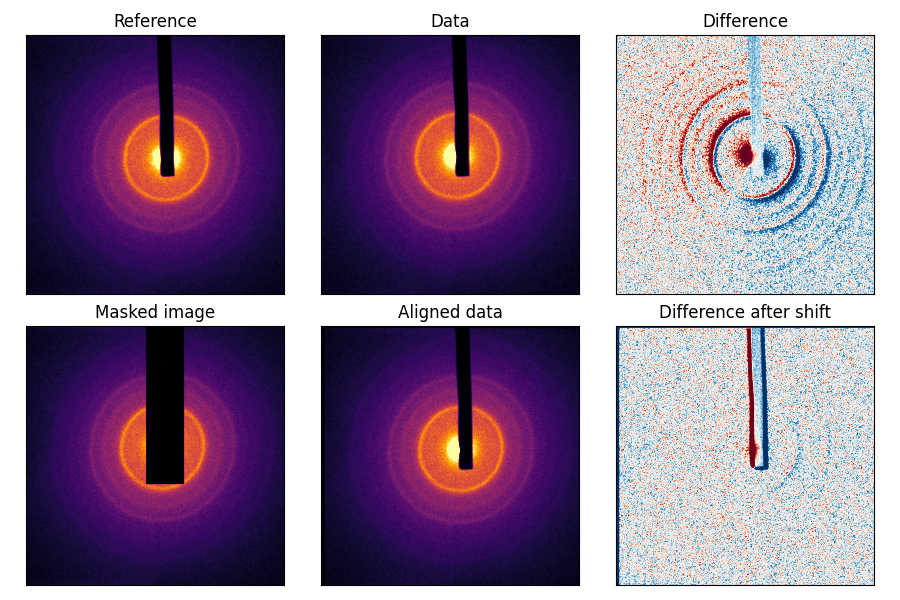
Thanks to the work of Dr. Dirk Padfield^{2 3}, we now know that such an operation exists: the masked normalized cross-correlation. In his 2012 article, he explains the procedure and performance of this method to register images with masks. One such example is the registration of ultrasound images; unfortunately, showing you the figure from the article would cost me 450 $US, so you’ll have to go look at it yourselves.

In order to fix our registration problem, then, I implemented the masked normalized cross-correlation operation — and its associated registration function — in our ultrafast electron diffraction toolkit, scikit-ued⁴. Here’s an example of it in action:

Contributing to scikit-image

However, since this tool could see use in a more general setting, I decided to contribute it to scikit-image:

1. My contribution starts by bringing up the subject via a GitHub issue (issue #3330).
2. I forked scikit-image and integrated the code and tests from scikit-ued to scikit-image. The changes are visible in the pull request #3334.
3. Finally, some documentation improvements and an additional gallery example were added in pull request #3528.

In the end, a new function has been added, skimage.registration.phase_cross_correlation (previously skimage.feature.masked_register_translation).