{-# LANGUAGE DataKinds #-}
{-# LANGUAGE OverloadedStrings #-}
{-# LANGUAGE TypeFamilies #-}
-- Suppress some warnings which take away from the beauty
-- of the post
{-# OPTIONS_GHC -Wno-missing-signatures #-}
{-# OPTIONS_GHC -Wno-missing-exported-signatures #-}
module GeneratingAClient where

import ApiAsType
    ( (:>),
      (:<|>)(..),
      Capture,
      Get,
      Post,
      QueryParam,
      ReqBody,
      Temperature
    )
import Control.Monad.IO.Class (liftIO)
import Control.Monad.Trans.Reader (ReaderT (runReaderT), ask)
import Data.ByteString (ByteString)
import Data.ByteString.Char8 qualified as BS
import Data.Data (Proxy (Proxy))
import Data.Function ((&))
import Data.Functor ((<&>))
import Data.List (intercalate)
import Data.Time (Day, fromGregorian)
import GHC.TypeLits (symbolVal, KnownSymbol)
import Network.HTTP.Client qualified as HTTP
import ServingAnApi (API)

Here we are. This is the moment I have been writing for, the end-game. After the last post, where we learned how to serve an API while having the compiler enforce the specs of said API, we are ready to generate client functions to query that same API.

The first time I saw this in action, I felt a combination of confusion and awe. In memory of this moment, I’ll just start by the end. Behold:

(forecastLastUpdated :<|> forecastAtDate) :<|> (getTemperature :<|> postTemperature) = client (Proxy :: Proxy API)

where forecastLastUpdated, forecastAtDate, getTemperature, and postTemperature are normal Haskell functions that allow us to interact with any server serving the API whose specification respects API, which, as a reminder, is:

type ForecastAPI =
        "forecast"
            :> ( "lastupdated" :> Get UTCTime
            :<|> Capture "date" Day :> "temperature" :> Get Temperature
               )

type WeatherAPI =
    "weather"
        :> "temperature"
            :> ( QueryParam "city" City :> Get Temperature
            :<|> Capture "city" City :> ReqBody Temperature :> Post
               )

type API = ForecastAPI :<|> WeatherAPI

• “Big deal bud, ever heard of OpenAPI?”

OpenAPI is nice, but, it’s also not enough. It’s hard to encode some invariants in an OpenAPI spec. In the set of languages that have an OpenAPI generator, the level of type sophistication ranges from “huh, types?” to Haskell. OpenAPI sacrifices some of the possible nuances by being more broadly usable.

So, how does this all work? Let’s find out.

What does one need, in order to interact with an HTTP API? It needs to know:

• What’s the hostname, port number, and possibly path where the server can be accessed;
• What the endpoints are;
• What shape does the requests and responses have, for a given endpoint.

We’ll tackle the first point first. When interacting with the API, some knowledge must come externally. We’ll store this information in its own environment type, ClientEnv:

data ClientEnv = ClientEnv
               { hostName :: String              -- ^ E.g. http://api.server.com
               , portNumber :: Int               -- ^ E.g. 80
               , basePath :: String              -- ^ E.g. /v1
               , networkManager :: HTTP.Manager  -- ^ To make network calls
               }

To promote re-use, we’ll package this data into a monad type that had ClientEnv as a static environment:

type ClientM a = ReaderT ClientEnv IO a

runClientM :: ClientEnv -> ClientM a -> IO a
runClientM = flip runReaderT

Now, if you recall the previous post in this series, we know what “shape” should the client functions be, and by shape, I mean the types. So, it’s going to be relatively straightward to say that, for example, the forecastLastUpdated client function should look like:

forecastAtDate :: Day -> ClientM Temperature

But, unlike serving the API, we’d like to also define the logic of the client function. Recall that a client function is basically assembles a request to be sent; we’ll chase that thought. Consider a very simple request type like so:

data Req = Req
         { reqBody   :: Maybe String       -- ^ Optional body of the request
         , reqParams :: [(String, String)] -- ^ Key-value pairs of query parameters
         , reqVerb   :: ByteString         -- ^ "GET" or "POST". If unset, the request is not valid.
         , reqPath   :: [String]           -- ^ Path to the endpoint from the base path
				                                   --   of the API, e.g. `["forecast", "2025-12-01", "temperature"]`
         }

Note that I’m being quite sloppy here. For example, we should make reqVerb take a sum type rather than any ByteString, but I’m trying to keep things as simple as possible.

We’ll walk through endpoints and construct client functions that, well, construct Reqs. Then, we can combine a Req with the ClientEnv to send a HTTP request. Let’s go!

As we have done three times already, we will express the functionality we want to add to the API type with a typeclass:

class HasClient api where
    type Client api

    clientWithRoute :: Proxy api -> Req -> Client api

Before we start writing instances, we’ll make some helper functions to make it easier to deal with Req. First, the empty request:

emptyReq :: Req
emptyReq = Req {reqBody = Nothing, reqParams = [], reqVerb = mempty, reqPath = []}

We need a way to set the body of the request. Recall that for simplicity, we assume that requests are all plaintext encoded, and so we serialize Haskell datatypes over the wire using the Show typeclass:

setBody :: Show a => a -> Req -> Req
setBody body req = req{reqBody = Just (show body)}

We also need to be able to set the verb of the request – actually, requests are invalid without a verb! You’ll see later how we enforce that all Reqs that get sent off have a valid verb later:

setVerb :: ByteString -> Req -> Req
setVerb verb req = req{reqVerb = verb}

We also need to add query parameters:

addQueryParam :: Show a => String -> a -> Req -> Req
addQueryParam key val req = req {reqParams = reqParams req <> [(key, show val)]}

and we need to be able to extend the path of the endpoint to which the Req is sent:

addToPath :: String -> Req -> Req
addToPath segment req = req{reqPath = reqPath req <> [segment]}

Finally, we also need a method for sending the request, and receiving the payload. We’ll re-use a low-level library for this, http-client:

toRequest :: Req -> ClientEnv -> HTTP.Request
toRequest (Req body params verb path) (ClientEnv hostname portnumber basepath _)
    = HTTP.defaultRequest { HTTP.method = verb
                          , HTTP.host = BS.pack hostname
                          , HTTP.port = portnumber
                          , HTTP.path = BS.pack $ basepath <> intercalate "/" path
                          , HTTP.queryString = BS.pack
                                             $ intercalate "&" [ key <> "=" <> val
                                                               | (key, val) <- params
                                                               ]

                          , HTTP.requestBody = HTTP.RequestBodyBS (maybe mempty BS.pack body)
                          }


runRequestNoBody :: Req -> ClientM ()
runRequestNoBody req = do
    clientEnv@(ClientEnv _ _ _ networkManager) <- ask
    liftIO (HTTP.httpNoBody (toRequest req clientEnv) networkManager) <&> HTTP.responseBody

runRequest :: Read a => Req -> ClientM a
runRequest req = do
    clientEnv@(ClientEnv _ _ _ networkManager) <- ask
    liftIO (HTTP.httpLbs (toRequest req clientEnv) networkManager)
        <&> HTTP.responseBody
        <&> BS.toStrict
        <&> BS.unpack
        <&> read

With these helper functions out-of-the-way, we can proceed with the real meat of this post. We start with terminal verbs. Recall that, for simplicity, we assume that all POST responses do not carry a body; hence, the client function must return ():

instance HasClient Post where
    type Client Post = ClientM ()

    clientWithRoute _ req = runRequestNoBody (req & setVerb "POST")

Side note: I love & and <&> and I wish to see it more. Moving on to GET:

instance Read a => HasClient (Get a) where
    type Client (Get a) = ClientM a

    clientWithRoute _ req = runRequest (req & setVerb "GET")

Get is a little more interesting because we have to specify a return type. Given our API specification, the parsing of the response body should never fail due to an unexpected type.

Let’s do ReqBody now. A client function for an endpoint using ReqBody a should supply the request with a body of type a; this means adding an argument to the client function, like we did for server handlers:

instance Show a => HasClient (ReqBody a :> sub) where
    type Client (ReqBody a :> sub) = a -> Client sub

    clientWithRoute _ req = ...

… wait, what should we write for clientWithRoute? Well, in this instance, clientWithRoute :: Proxy ... -> Req -> Client (ReqBody a :> sub), which is

clientWithRoute :: Proxy (ReqBody a :> sub)
                -> Req
                -> (a -> Client sub)

Since ReqBody never appears at the end of an endpoint definition, we must recur with clientWithRoute. This also requires us to make sure that the sub-API, sub, is an instance of HasClient:

instance (HasClient sub, Show a) => HasClient (ReqBody a :> sub) where
    type Client (ReqBody a :> sub) = a -> Client sub

    clientWithRoute _ req body = clientWithRoute (Proxy :: Proxy sub) (setBody body req)

Great! Let’s do QueryParam. Recall that in our implementation, a query parameter is always optional. Recall that in QueryParam name a, name is a type-level string which we can bring to the values world by using symbolVal:

instance (HasClient sub, KnownSymbol name, Show a) => HasClient (QueryParam name a :> sub) where
    type Client (QueryParam name a :> sub) = Maybe a -> Client sub

    clientWithRoute _ req param =
        clientWithRoute
            (Proxy :: Proxy sub)
            (addQueryParam
                (symbolVal (Proxy :: Proxy name))
                param
                req
            )

After this, a Capture is going to be easy:

instance (HasClient sub, Show a) => HasClient (Capture name a :> sub) where
    type Client (Capture name a :> sub) = a -> Client sub

    clientWithRoute _ req capture =
        clientWithRoute
            (Proxy :: Proxy sub)
            (addToPath (show capture) req)

We’re almost done. Path segments only add the the path of the request, but otherwise do not add a parameter to our client function:

instance (HasClient sub, KnownSymbol segment) => HasClient (segment :> sub) where
    type Client (segment :> sub) = Client sub

    clientWithRoute _ req
        = clientWithRoute
            (Proxy :: Proxy sub)
            (addToPath (symbolVal (Proxy :: Proxy segment)) req)

Finally, the ever-interesting (:<|>) instance. In this case, no thought is required, since there’s only one thing that will type-check:

instance (HasClient left, HasClient right) => HasClient (left :<|> right) where
    type Client (left :<|> right) = Client left :<|> Client right

    clientWithRoute _ req
        =    clientWithRoute (Proxy :: Proxy left) req
        :<|> clientWithRoute (Proxy :: Proxy right) req

Not that much work! How do we connect HasClient with our first demonstration of the function client? Behold:

client :: HasClient api => Proxy api -> Client api
client proxy = clientWithRoute proxy emptyReq

In action, here’s how we can fetch the forecasted temperature on Christmas:

run :: IO ()
run = do
    networkManager <- HTTP.newManager HTTP.defaultManagerSettings
    let clientEnv = ClientEnv
                  { hostName = "myserver.com"
                  , portNumber = 80
                  , basePath = "/api"
                  , networkManager = networkManager
                  }

        christmasDay = fromGregorian 2025 12 25

    runClientM clientEnv (forecastAtDate christmasDay) >>= liftIO . print

forecastAtDate is just a regular function, but there’s a lot going on under the hood!

Automatically generating client functions for an API is beautiful. It looks like magic, but when we look under the hood, it’s “““just”“” type families, partially-applied functions, Proxy, and recursion.

Unlike the previous posts, the code above is NOT a highly simplified version of what Servant provides for real clients via servant-client. The only thing we’re missing here is support for the real Servant combinators (powering authentication, streaming, HTTP headers, etc), and allowing for other base monads than IO. That’s not bad!

Today, we do some real web development stuff: we’ll go too far building abstractions we’ll serve an API.

This file is a Literal Haskell module, so we need to get some imports out-of-the-way.

{-# LANGUAGE DataKinds #-}
{-# LANGUAGE OverloadedStrings #-}
{-# LANGUAGE TypeFamilies #-}
module ServingAnApi where

import ApiAsType
    ( (:>),
      (:<|>)(..),
      Capture,
      City,
      Get,
      Post,
      QueryParam,
      ReqBody,
      Temperature (MkTemperature),
    )
import Data.Data (Proxy (..))
import Data.Kind (Type)
import Data.Text qualified as Text
import Data.Text.Encoding qualified as Text
import Data.ByteString.Lazy qualified as ByteString
import Data.ByteString.Char8 qualified as ByteString.Char8
import Data.Time (UTCTime, Day)
import Data.Time qualified
import GHC.TypeLits (KnownSymbol, symbolVal)
import Network.Wai.Internal (Request(..), Response(..))
import Network.Wai (Application, responseLBS, strictRequestBody)
import Network.Wai.Handler.Warp qualified as Warp
import Network.HTTP.Types qualified as HTTP

So, recall from the first post in this series, that we have an API we have modelled:

type ForecastAPI =
        "forecast"
            :> ( "lastupdated" :> Get UTCTime
            :<|> Capture "date" Day :> "temperature" :> Get Temperature
               )

type WeatherAPI =
    "weather"
        :> "temperature"
            :> ( QueryParam "city" City :> Get Temperature
            :<|> Capture "city" City :> ReqBody Temperature :> Post
               )

type API = ForecastAPI :<|> WeatherAPI

This API, represented by the API type, has 4 endpoints, split into two sub-APIs, one for forecasting (ForecastAPI) and one for real-time weather measurements (WeatherAPI). We want to write a server application to serve this API.

Now, life is short, priorities already changed twice this sprint, and I don’t like debugging production issues, so we’ll add one more requirement: we want to enforce, at compile-time, that our server application respects our API specification. Let’s go!

Our API specification has 4 endpoints. So, our server application should be composed of 4 functions somehow; each function is the handler for a request to an endpoint. If you forget the details of our API and label the endpoints a, b, c, and d, we need four handler functions ha, hb, hc, and hd for endpoints a, b, c, and d respectively.

This relationship between an endpoint and its handler function isn’t the kind of loving, nurturing relationship you witness on Love Island: it’s entirely dictated by whatever the endpoint specification says. What I mean is that there’s only one handler function that respects any given endpoint specification. We’ll encode this relationship from endpoint to handler function as a function.

Wait a minute, I hear you say. The endpoint specification is a type, and a handler function also has a type. How can this be encoded in a function? Well, the de-facto standard Haskell compiler, GHC, has a feature called type families, which can be used to model type-level functions. I have written about type families before^{1 2}; I’ll assume that you have an understanding of how they work.

So, just like in our previous post, we will build up a result type (in this case, the type of a server) by walking over the structure of an API type. As you may remember, case-by-case analysis on types can be represented by a typeclass in Haskell. I posit that the following typeclass does it:

class HasServer a where
    type Server a

That is, for each component type of our API (like Get and Capture), we will have an associated type Server a, the type of the server for the part of the API which is a. It looks like I’m being loose with language here, but I am not: an endpoint has a handler function, but a whole API has a server. It just so happens that if the API is a single endpoint, then the server is also just a handler function.

As before, we will recursively build the Server type for our API type, Server API, by composing the Server for our components. We start with the base case, the return type of an endpoint which is given by the terminal verbs:

instance HasServer Post where
    type Server Post = IO ()

This is pretty straightforward: in our implementation, for simplicity, the Post terminal verb never returns any data. Therefore, the handler function for a Post should return nothing, labeled as (). Note that we make our server implementation run in the IO monad; this is more realistic, as it allows us to do some side effects like interact with a database.

Let’s move on to Get. The handler function for a Get endpoint returns data:

instance HasServer (Get a) where
    type Server (Get a) = IO a

Sike, this won’t compile. Haskell is so flexible that the compiler can’t know if a is a type (which can be returned by a function), or something higher-kinded (which cannot be returned by a function). For example, what if a = Proxy? That’s not a type – Proxy is partially-applied, so-to-speak! Therefore, we must be more specific by saying that a must be a concrete type. Behold:

instance HasServer (Get (a :: Type)) where
    type Server (Get a) = IO a

I sure hope that’s the last technicality we encounter!

Moving on to other component types, you’ll notice that none can be in the end position of an endpoint. This is important: it means that all further definitions of Server will recur!

Let’s move on to ReqBody:

instance HasServer sub => HasServer (ReqBody (a :: Type) :> sub) where
    type Server (ReqBody a :> sub) = ...

We have to think about this. Clearly, the left hand side must involve a and Server sub somehow. We compose API components using (:>) or (:<|>). We composed the implementations of toLink using recursive function calls. How are we supposed to compose the types here? Since the resulting type of Server should be a handler function, we should probably compose Server (ReqBody a) and Server sub such that they form a function. Well, the composition of types into a function, in Haskell, is done with (->)!

instance HasServer (ReqBody (a :: Type) :> sub) where
    type Server (ReqBody a :> sub) = a -> Server sub

This makes intuitive sense: the handler function for an endpoint which has a request body of type a, should take a as an argument. Right on!

We move to QueryParam. Recall that we defined our query parameters to be optional, which means that our handler function must take in Maybe a as an argument, not a directly:

instance HasServer (QueryParam name (a :: Type) :> sub) where
    type Server (QueryParam name a :> sub) = Maybe a -> Server sub

Great, I’m getting used to this. Now, let’s do path segments. That’s easy, since they don’t affect the logic of our handler function, only the routing of requests (which we will get to later in this post):

instance KnownSymbol segment => HasServer (segment :> sub) where
    type Server (segment :> sub) = Server sub

Now we do Capture. Just like ReqBody, this is required and should be a function argument. Therefore:

instance HasServer (Capture name (a :: Type) :> sub) where
    type Server (Capture name a :> sub) = a -> Server sub

Finally, we have (:<|>). This is the composition of two handler functions, or two subservers, for two parts of an API, into a true server. We’ll keep this simple for now, and you’ll see how we use it in practice:

instance HasServer (a :<|> b) where
    type Server (a :<|> b) = Server a :<|> Server b

We did all this work… can we serve that API yet?! Don’t be so hasty. Look at the scrollbar, we’re barely halfway. We need to deal with one more piece of the puzzle: routing requests to the right handler.

To route requests, we need to understand the high-level structure of a server. A web server is a program which looks like Request -> IO Response

We re-use the Haskell Web Application Interface types Request and Response, like Servant and many other Haskell web frameworks also do. Now, the question is: which handler function gets the Request, and thus provides the Response? We need to introduce a method to say whether a handler function matched a route (and thus should process the request), or if the route does not match, in which case another handler function must be tried. We do so using as sum type:

data RouteResult a
    = Matched a
    | NotMatched

Now, for every part of our API, we want to determine a function of type Request -> IO (RouteResult Response). We will look through the API for the first handler function which returns a Matched Response!

As we’ve done twice now with HasLink and HasServer, we package the functionality in a class, HasRoute:

type RoutingApplication = Request -> IO (RouteResult Response)

class HasRoute api where
    route :: Proxy api -> Server api -> RoutingApplication

Recall that we need to use Proxy here because otherwise the type inference won’t work. Yes, even if Server api appears in the type signature, because Server api is a type function whose result is probably not related directly to api!

The plan is to look at the path of the request, and recursively match its content to find the right part of the API for which to return Matched. As we’ve done twice now, we start with the terminal verbs:

buildResponse :: Show a => a -> Response
buildResponse = responseLBS HTTP.status200 mempty . ByteString.fromStrict . Text.encodeUtf8 . Text.pack . show

instance Show a => HasRoute (Get (a :: Type)) where
    route (Proxy :: Proxy (Get a)) (handler :: IO a) = \request ->
        if (requestMethod request == "GET" && null (pathInfo request))
            then Matched . buildResponse <$> handler
            else pure NotMatched

Oof. A couple of things to note. The first is that, as you can see by our definition of buildResponse, we are modeling a very simple server: a server that never fails (I wish), and thus always returns HTTP200 status codes if a handler is found. Second, the payload of all responses is serialized from the Show instance. This is all in the name of simplicity. In a subsequent post, I may show you how Servant deals with content types – send me an e-mail if you’d like to read that!

The logic of this instance isn’t particularly complex: if the request is a GET request, and we’ve consumed all of its path (and therefore it is the empty list, hence null returns True), then our handler function has indeed matched this route, and we return the result of action as Matched <the response>. I have annotated handler with the type; recall that Server (Get a) === IO a! Otherwise, this handler is NOT the right handler for this request.

The instance for Post is basically similar, but the response is empty (again, to keep things simple). I’ll stop writing out Proxy everywhere, and replace it by _:

instance HasRoute Post where
    route _ (handler :: IO ()) = \request ->
        if (requestMethod request == "POST" && null (pathInfo request))
            then Matched . buildResponse <$> handler
            else pure NotMatched

Let’s move on to ReqBody. This is the first case where we will recur:

readReqBody :: Read a => Request -> IO a
readReqBody req = read . Text.unpack . Text.decodeUtf8Lenient . ByteString.toStrict <$> strictRequestBody req

instance (Read a, HasRoute sub) => HasRoute (ReqBody (a :: Type) :> sub) where
    route _ handler = \request -> do
        readReqBody request >>=
            \body -> route (Proxy :: Proxy sub) (handler body) request

There’s a lot going on here! First, we read the body of the request using readReqBody, assuming it is plaintext and always succeeds (insert sarcastic comment). We then pass the parsed body down the routing tree, where the body is used by the handler. One subtle, but awesome, thing to see here is that handler may be a function with lots of arguments – results of query parameters and capture parameters – so handler body could be a partially-applied function!

Time for QueryParam, which are always optional. Just like ReqBody, we don’t bother parsing the data properly, and use read for simplicity:

readQueryParam :: Read a => String -> HTTP.Query -> Maybe a
readQueryParam paramName query =
    let paramNameBytes = ByteString.Char8.pack paramName
    in lookup paramNameBytes query
        >>= fmap (read . ByteString.Char8.unpack)

instance (KnownSymbol name, Read a, HasRoute sub) => HasRoute (QueryParam name (a :: Type) :> sub) where
    route _ handler = \request ->
        let (queryParam :: Maybe a) = readQueryParam (symbolVal (Proxy :: Proxy name)) (queryString request)
        in route (Proxy :: Proxy sub) (handler queryParam) request

Recall from the last post, that we can use symbolVal to extract the string associated with a type-level string (in this case, name). That name is used to lookup the value of the appropriate query parameter stored in the HTTP.Query, if it is found. Just like with ReqBody, the parsed value, queryParam, is passed to the handler, which may be a partially-applied function!

Onto path segments. As you can imagine, they contribute to routing but handlers are unmodified. A path segment which matches the begining of the request path will continue to route, while if the path segment doesn’t match, we return NotMatched. The key to recursive behavior here is to remove the prefix of the request path on successful match, such that the next segment only has to match the prefix of the path.

instance (KnownSymbol segment, HasRoute sub) => HasRoute (segment :> sub) where
    route _ handler = \request ->
        let apiSegment = Text.pack $ symbolVal  (Proxy :: Proxy segment)
        in case pathInfo request of
            [] -> pure NotMatched
            (nextSegment:rest) ->
                if  nextSegment == apiSegment
                    then route (Proxy :: Proxy sub)
                           handler
                           (request{pathInfo = rest})
                    else pure NotMatched

Now path captures. We’re not going to re-invent the wheel here, using the Read instance on the path, and assuming it always succeeds:

readCapture :: Read a => String -> a
readCapture = read

instance (Read a, HasRoute sub) => HasRoute (Capture name (a :: Type) :> sub) where
    route _ handler = \request -> case pathInfo request of
        [] -> pure NotMatched
        (value:rest) ->
            let captureParam = readCapture (Text.unpack value)
            in route (Proxy :: Proxy sub)
                     (handler captureParam)
                     (request{pathInfo = rest})

Finally, we have (:<|>). This is relatively straightforward: we try the left branch, and return the result of that handler if it returns Matched. Only if the left branch returns NotMatched do we even try the right branch. There’s one interesting tidbit, though: the type function Server (left :<|> right) is a structure of functions, Server left :<|> Server right. This means that the handler we’re using on either branch is of the correct type, always!

instance (HasRoute left, HasRoute right) => HasRoute (left :<|> right) where
    route _ (leftHandler :<|> rightHandler) = \request -> do

        let tryLeft  = route (Proxy :: Proxy left) leftHandler
            tryRight = route (Proxy :: Proxy right) rightHandler

        leftMatch <- tryLeft request
        case leftMatch of
            Matched result -> pure $ Matched result
            NotMatched -> tryRight request

I’d like you to know that it was very hard to resist refactoring this to use Alternative, but this post is already getting long.

Now we have the appropriate blocks to serve our API. In case none of the routes match, we need to build a HTTP404 response:

notFound :: Response
notFound = responseLBS HTTP.status404 mempty mempty

and beyond this, we just need to provide the Server api structure to a new function, serve:

serve :: (HasServer api, HasRoute api)
      => Proxy api
      -> Server api
      -> (Request -> IO Response)
serve proxy server = \request -> do
    result <- route proxy server request
    case result of
        Matched response -> pure response
        NotMatched -> pure notFound

So, what does Server api look like? Well, it’s a structure of handler functions, one for each endpoint. We’ll write them all out with trivial logic:

-- To serve GET /forecast/lastupdated
forecastLastUpdated :: IO UTCTime
forecastLastUpdated = Data.Time.getCurrentTime

-- To serve GET /forecast/<date>/temperature
forecastTemperatureAtDate :: Day -> IO Temperature
forecastTemperatureAtDate _ = pure $ MkTemperature 0

-- To serve GET /weather/temperature&city=<city>
temperatureAtCity :: City -> IO Temperature
temperatureAtCity _ = pure $ MkTemperature 0

-- To serve POST /weather/temperature/<city>
recordTemperatureAtCity :: City -> Temperature -> IO ()
recordTemperatureAtCity _ _ = pure () -- This is technically ACID-compliant

We need to combine these four handlers in the same way that the endpoints are structured:

apiServer :: Server API
apiServer =
    let forecastAPI = forecastLastUpdated :<|> forecastTemperatureAtDate
        weatherAPI = temperatureAtCity :<|> recordTemperatureAtCity
    in forecastAPI :<|> weatherAPI

If you try this, you’ll get a compilation error! This actually happened as I was writing this blog post; I forgot that QueryParam in temperatureAtCity is actually optional! The type checker has my back, even when writing blog posts. Instead, I need to write:

temperatureAtCityCorrect :: Maybe City -> IO Temperature
temperatureAtCityCorrect _ = pure $ MkTemperature 0

apiServer :: Server API
apiServer =
    let forecastAPI = forecastLastUpdated :<|> forecastTemperatureAtDate
        weatherAPI = temperatureAtCityCorrect :<|> recordTemperatureAtCity
    in forecastAPI :<|> weatherAPI

Now it compiles. Let’s pull things all together:

myServer :: Request -> IO Response
myServer = serve (Proxy :: Proxy API) apiServer

Now that we have our server logic, we defer the parsing of requests, networking, and other low-level concerns to a lower-level server runner (in this case, warp). Our executable becomes:

-- We convert our handler function to a WAI application, which is slightly
-- different for better resource management (not applicable here)
toApplication :: (Request -> IO Response) -> Application
toApplication handler = \request respond -> handler request >>= respond

runServer :: IO ()
runServer = Warp.run 80 (toApplication myServer)

And voilà! We built a real HTTP web application using our simplified, homegrown version of Servant. This web server respects the API specification not out of politeness, but out of coercion by the compiler. Amazing!

The code above is admittedly a highly simplified version of what a production-ready web framework should be. Some of the differences between what I’ve shown you here and the real Servant include:

• Dealing with more failure modes;
• Dealing with content-types. Real Servant API specifications encode the accepted content-types, and automatically parse requests and serializes responses based on the type-level description of content types;
• Sublinear routing. Our routing algorithm finds a route in linear time, but the real Servant is a lot more clever;
• Support for more sophisticated API components, such as streaming endpoints and authentication;
• Running handler functions in monads other than IO. This is a big deal if you have to wrangle side effects related to a database, logging facilities, OpenTelemetry, etc.

The next post is the last planned post in this series. It’ll deal with automatic derivation of client functions to query a server. See you soon!

I know, this isn’t mindblowing, but it will require the use of a basic technique that most Servant functionality uses: the Proxy type. This tool (and others!) will be used again and again as we re-build more powerful components of Servant.

This file is a Literate Haskell module, so we have to get some ceremony out-of-the-way.

{-# LANGUAGE DataKinds #-}
module TypeSafeLinks where

-- From the previous post in this series
import ApiAsType
    ( (:>),
      Capture,
      City,
      Get,
      Post,
      QueryParam,
      ReqBody,
      Temperature,
    )

-- we'll need these later on
import Data.List (intersperse)
import Data.Proxy (Proxy(..))
import Data.Time (Day)
import GHC.TypeLits (KnownSymbol, symbolVal)

Here’s what we want to do: given the type associated with an endpoint, we want a string that represents a universal resource identifier to this endpoint, in the form of a link¹.

Simply put, for every segment of an endpoint, we want a piece of string that represents it. For example, the endpoint represented by the type

type ForecastLastUpdated = "forecast" :> "lastupdated" :> Get UTCTime

should give us the link

"/forecast/lastupdated"

, while the endpoint represented by the type

type ForecastTemperature = "forecast" :> Capture "date" Day :> "temperature" :> Get Temperature

should give us the link

"/forecast/<date>/temperature"

Recall that the segments "forecast", "lastupdated", and "temperature" are type-level strings, or Symbols. The links, such as "/forecast/lastupdated", will be represented by term-level strings:

type Link = [String]

Before we break out the advanced type stuff, let’s build this functionality as if we represented our API not with a type, but with data. We’ll focus on only one of the endpoints, specifically the endpoint given by the type:

type ForecastLastUpdated = "forecast" :> "lastupdated" :> Get UTCTime

Imagine if we instead represented that endpoint using the following construction:

data APIComponent
    = Get
    | Segment String
    | Join APIComponent APIComponent

exampleEndpoint :: APIComponent
exampleEndpoint = Segment "forecast" `Join` Segment "lastupdated" `Join` Get

Extracting the link from such a value can be done recursively:

endpointLink :: APIComponent -> Either String Link
endpointLink = fmap (intersperse "/") . go [root]
  where
    root :: String
    root = "/"

    go :: Link -> APIComponent -> Either String Link
    go accumulator Get = Right accumulator
    go accumulator (Join (Segment segment) component) =
        go (accumulator <> [segment]) component
    -- Any other structure is considered a malformed API
    go _ _ = Left "Endpoint structure doesn't make sense"

(Sidenote: please forgive me for appending to a linked list; I’m trying to keep things as simple as possible.)

The result would be:

 ghci> endpointLink exampleEndpoint
 "/forecast/lastupdated"

The key concept in endpointLink is that we recursively walk over the parts of the endpoint until we hit a verb, in this case Get, while accumulating parts of the link. When we build this functionality for type-level API definitions, we’ll do something very similar: we’ll walk over all components of the API type with a function, accumulating parts of the link, until we hit a terminal verb.

Note that we had to handle the case of nonsensical API structures at runtime. In this case, the only valid API are those composed of zero or more Segments ultimately ending in Get, all joined with Join. Any other structure results in an error, represented by Left "...".

Let’s move back to the world of APIs defined as types.

The component of an API type, like Capture or a type-level symbol "forecast", is associated with zero or more segments. This type-level “case-by-case” is the realm of typeclasses. We want to create a typeclass, and apply it recursively over our API type, building from the base link "/" incrementally. Let’s try to create this typeclass:

class HasLink1 endpoint where
    toLink1 :: Link -- ^ base link, initially just "/"
            -> Link

-- Example
instance HasLink1 "forecast" where
    toLink1 :: Link -> Link
    toLink1 baselink = [baselink, "forecast"]

Unfortunately, this is not going to compile. The problem is that type inference won’t work; given a toLink1 in the middle of a Haskell file, how can the compiler know which endpoint type it refers to? It can’t know. We need to inject type information in the signature of toLink1.

How about this?

class HasLink2 endpoint where
    toLink2 :: Link -- ^ base link
            -> endpoint
            -> Link

This would work, if we could construct a term of type endpoint… which we can’t, since many of our API component types, like Get a, don’t have constructors. The API component types are entirely for type-level computation; we can’t construct values for them by design.

So, how do we inject type information, without an associated value? Put down that undefined ಠ_ಠ we don’t do that here. Being respectable, modern Haskellers, we’ll reach for Proxy. Proxy is a higher-kinded type that allows us to carry a type witness, without having to construct any values (since the Proxy constructor takes no parameter). It’s defined like so:

data Proxy a = Proxy

We can now reformulate our class as the final, correct version:

class HasLink endpoint where
    toLink :: Proxy endpoint
           -> Link -- ^ Base link
           -> Link

where the use of Proxy will allow the compiler to infer type information.

Now, we need to write typeclass instances of the class HasLink for all of the building blocks that make up our API. The easiest instances of HasLink are for the terminal verbs, as they do not appear in the endpoint link:

instance HasLink (Get a) where
    toLink :: Proxy (Get a) -> Link -> Link
    toLink _ baselink = baselink

instance HasLink Post where
    toLink :: Proxy Post -> Link -> Link
    toLink _ baselink = baselink

There’s something else about the terminal verbs, Get and Post: we expect them at the end of our endpoint. There’s no recursion inside toLink here, because by definition, the description of an endpoint as a type always ends in Get or Post. These are the base cases.

On the other hand, query parameters and POST request bodies don’t appear in the endpoint link either, but cannot be placed at the end position of the endpoint definition; they are always contained in a (:>):

instance HasLink sub => HasLink (ReqBody b :> sub) where
    toLink :: Proxy (ReqBody b :> sub) -> Link -> Link
    toLink _ = toLink (Proxy :: Proxy sub)

instance HasLink sub => HasLink (QueryParam name a :> sub) where
    toLink :: Proxy (QueryParam name a :> sub) -> Link -> Link
    toLink _ = toLink (Proxy :: Proxy sub)

Here, we see something different than for Get and Post: the definition of toLink recurs as it moves along the endpoint type.

Let’s pause here for a second, because there’s something very cool that’s easy to miss: we can control what a valid API looks like by NOT writing instances for HasLink. For example, it doesn’t make sense to create a link to something involving :<|>; for example, left :<|> right is for composing endpoints left and right into an API, but there’s no link that makes sense for left :<|> right itself. Well, if we don’t write an instance HasLink (a :<|> b), we’ll never be able to construct a link to a malformed endpoint, because toLink won’t compile! We’ve transformed the runtime error (Left "...") from our function endpointLink above, into a compile-time error. How awesome is that?!

Let’s climb down from this apotheosis, as it were, and move to the HasLink instance for the path components of endpoints, for which we’ve been using Symbol. Obviously, the type ("some-string" :: Symbol) should result in the link fragment ("some-string" :: String) somehow. This is one of the advantages of using Symbol: we can use symbolVal to get the value representation of the type-level string, which itself uses the KnownSymbol constraint:

instance KnownSymbol endpoint => HasLink endpoint where
    toLink proxy baselink = baselink <> [symbolVal proxy]

This is a somewhat complicated way of saying that the following example holds:

toLink (Proxy :: Proxy ("endpoint" :: Symbol)) ["/"] == ["/", "endpoint"]

where Proxy "endpoint" contains the type-level string "endpoint", while the right-hand side ["/", "endpoint"] is a regular value of type [String].

With this out of the way, we can write instances for all other types of our API. <some symbol> :> subapi is an interesting one because we recursively use toLink forwards and backwards:

instance (KnownSymbol super, HasLink sub) => HasLink (super :> sub) where
    toLink (Proxy :: Proxy (super :> sub)) baselink
        =  toLink (Proxy :: Proxy super) baselink -- backwards
        <> toLink (Proxy :: Proxy sub) []         -- forwards

For example:

toLink (Proxy :: Proxy ("forecast" :> "lastupdated")) ["/"] == ["/", "forecast", "lastupdated"]

Capture is last, and we get to re-use symbolVal. This is because we want to represent the name of the capture parameter, sandwiched between < and >:

instance (HasLink sub, KnownSymbol name) => HasLink (Capture name a :> sub) where
    toLink (Proxy :: Proxy (Capture name a :> sub)) baselink
        =  baselink
        <> ["<" <> symbolVal (Proxy :: Proxy name) <> ">"]
        <> toLink (Proxy :: Proxy sub) []

For example:

toLink (Proxy :: Proxy ("forecast" :> Capture "date" Day :> "temperature")) ["/"]
    == ["/", "forecast", "<date>", "temperature"]

We’re almost done. We’ll just wrap toLink to make it easier to use. In particular, we want to represent the list of link segments as a single piece of String:

safeLink :: HasLink endpoint => Proxy endpoint -> String
safeLink endpoint
    = mconcat
    $ intersperse "/"
    $ toLink endpoint ["/"]

and boom! We are ready to generate links to our type-leven endpoints. Behold:

 ghci> safeLink (Proxy :: Proxy ("forecast" :> Capture "date" Day :> "temperature" :> Get Temperature))
 "/forecast/<date>/temperature"
 ghci> safeLink (Proxy :: Proxy ("weather" :> "temperature" :> Capture "city" City :> ReqBody Temperature :> Post))
 "/weather/temperature/<city>"

This concludes our first derivation from an API that can be represented by types. This allowed us to create links to endpoints in our API, while ensuring that if an endpoint exists, links to it will be valid. Otherwise, we get a compile-time error!

I wanted to show you this first, because we got acquainted with Proxy, a type that is often seen to help with inference of complex types.

The constructs you have seen in this post are all part of the Servant codebase, although I have simplified things here. This includes safeLink, and the HasLink typeclass. The real safeLink function is notably more powerful for two reasons:

• You get a compile time error if the endpoint isn’t part of the given API. This means you get even more certainty that the link is valid;
• You can feed safeLink the values that go in Capture and QueryParam, to get the true link to the endpoint, rather than having e.g. a <date> placeholder.

In the next post, we will go one step further: checking the shape of the server handlers at compile-time. This will require us to use Proxy again, but we’ll also learn about how type families, or type functions, fit in all of this.

{-# LANGUAGE DerivingStrategies #-}
-- We'll get back to DataKinds
{-# LANGUAGE DataKinds #-}
module ApiAsType where

-- we'll need these later on
import Data.Text (Text)
import Data.Time (UTCTime, Day)
import GHC.TypeLits (Symbol)

A web application programming interface (API) can be represent by a tree of endpoints¹. The foundational idea behind Servant is that this tree of endpoints can be represented as one type. This API type is constructed by using higher-order types to compose endpoints together.

This foundational idea leads to most of Servant’s power. First, moving data into types helps tremendously with ensuring correctness, as we will soon see. Second, we can derive functionality on demand for our API type using typeclasses. This last sentence is wholly uninformative unless you already know Servant, so please bear with me here while we construct examples.

For the remainder of this blog series, we will consider an example, concrete API. This isn’t a lesson in API design. For simplicity, we assume that all data to and from the server will be encoded in plain text (although we may extend this in later posts).

The example API is a weather API which deals with measurements and forecasts of outdoor temperature. Here are the endpoints:

-- Returns the time at which forecasts we last updated.
GET /forecast/lastupdated

-- Returns the forecasted temperature on a (future) date for all known places.
-- The date is captured from the endpoint, e.g. "/forecast/2025-06-01/temperature"
-- should return the temperature forecasted for June 1st, 2025
GET /forecast/<date>/temperature

-- Returns the temperature on this current date. The city is expected to
-- be passed as a required query parameter, e.g. "/weather/temperature&city=Montreal"
GET /weather/temperature&city=<city>

-- Record a temperature measurement posted by someone for a given city
POST /weather/temperature/<city>

This example API has a good mixture of methods (GET and POST), query parameters, and path parameters. Let’s create some types to help us describe this API.

First, we want to extend routes. For example, /forecast/lastupdated and /forecast/<date>/temperature share the root forecast:

data a :> b

infixr 4 :>

Haskell is known for using all sorts of non-standard character sequences as functions, like (>>=). Well, you can do the same for types! Example usage for (:>):

data Forecast
data LastUpdated

type LastUpdatedForecast = Forecast :> LastUpdated

Wait a second – aren’t path segments strings, like "forecast" and "lastupdated"? Why isn’t the definition data String :> String? This is the power of Servant, but also the source of its complexity: APIs are meant to represented by types, that the compiler can check at compile-time. Instead of every piece of our API being a different string of the same type, they are all a different type. For now, trust me that this is worth doing.

APIs defined in Servant use tons of bespoke types, like Forecast and LastUpdated above. To save on the boilerplate of defining a bunch of these types, people typically use the DataKinds extension, which is enabled in this module. With it, instead of:

data Root
data Branch
data Leaf

type Tree1 = Root :> Branch :> Leaf

we can write:

type Tree2 = "root" :> "branch" :> "leaf"

"root", "branch", and "leaf" are type-level strings, which have kind Symbol, and you will see that they have advantages that we’ll see later on.

Allright, now we can compose path segments into long path segments using (:>). What about describing the endpoint? For example, GET /forecast/lastupdated should return the time at which the forecast was last updated. We can define a type to specify this:

data Get a

where a is the return type of this endpoint. At last, we can express the full type of one of our endpoints:

type GetForecastLastUpdated = "forecast" :> "lastupdated" :> Get UTCTime

You might be wondering why our Get doesn’t have a constructor. Why not:

data Get a = MkGet {unGet :: a}

The reason is that our API will not exist in this form at runtime. As you will see later on, we will derive things from our API, and these derivations will be used at runtime, but not the API itself.

Let’s tackle the second endpoint, GET /forecast/<date>/temperature. This endpoint is interesting because we want to capture some date, to be used when processing the request. To do this, we’ll create yet another type:

data Capture (name :: Symbol) a

where name will represent some parameter name, which will be useful later on, and a is the type being captured. Recall that in this case, name is a Symbol, or type-level string, and not a real String. Our GET /forecast/<date>/temperature can thus be represented by:

-- Type representing temperature in Celsius
newtype Temperature = MkTemperature Double
    deriving newtype (Eq, Show, Read, Num)

type GetForecastTemperature = "forecast" :> Capture "date" Day :> "temperature" :> Get Temperature

The two API endpoints we’ve defined so far, have the same root (forecast). It’s often useful to define relate endpoints sharing the same root together – for example, to define authentication which should apply to all related endpoints. We will create a type to represent the branching of endpoints:

data a :<|> b = a :<|> b

-- We want :<|> to have a lower precedence than :> so that we can
-- write API definitions without tons of parentheses
infixr 3 :<|>

With :<|>, we can write our forecast endpoints as :

type ForecastRoutes =
    "forecast" :>
            ( "lastupdated"
                    :> Get UTCTime
            :<|>
                Capture "date" Day
                    :> "temperature"
                        :> Get Temperature
            )

which is formatted to look like a tree:

forecast
 ├─lastupdated
 │  └─GET UTCTime
 └─<date>
    └─temperature
       └─GET Temperature

The next endpoint, GET /weather/temperature&city=<city>, has a new wrinkle: an (optional) query parameter. This warrants a new type:

data QueryParam (name :: Symbol) a

such that we can write:

newtype City = MkCity Text
    deriving newtype (Show, Read)

type GetTemperature = "weather" :> "temperature" :> QueryParam "city" City :> Get Temperature

For the last endpoint, POST /weather/temperature/<city>, we need two last constructs. In a POST request, the request body will contain some data for the server to process (in the case of our endpoint, this data will be a temperature measurement in plaintext). Moreover, in our example, the POST request will return no data. For our API description to be adequate, we must describe the request body and the lack of data returned with – you guessed it – new types:

data Post

data ReqBody a

The endpoint description becomes:

type PostTemperature = "weather" :> "temperature" :> Capture "city" City :> ReqBody Temperature :> Post

Let’s structure all of our endpoints into a single type:

type ForecastAPI =
        "forecast"
            :> ( "lastupdated" :> Get UTCTime
            :<|> Capture "date" Day :> "temperature" :> Get Temperature
               )

type WeatherAPI =
    "weather"
        :> "temperature"
            :> ( QueryParam "city" City :> Get Temperature
            :<|> Capture "city" City :> ReqBody Temperature :> Post
               )

type API = ForecastAPI :<|> WeatherAPI

Enough new types; let’s recap what we have created so far:

• We created a type :> to build endpoint paths from segments;
• We created a type :<|> to build branching paths;
• We created a type Capture to capture data in endpoint paths;
• We created a type QueryParam to specify the name and type of optional query parameters;
• We created a type ReqBody to specify the type of the body of a POST request;
• We created types Get and Post to represent the verb of a request;
• We created a type, API, built up from smaller types ForecastAPI and WeatherAPI, which can be used to describe all of our API.

It bears repeating: none of the types defined above have constructors, which means that the type of our API, API, cannot even be instantiated at runtime! All functionality that will have to do with our API will come from deriving things from its definition at compile time.

In the next post, we will start from the API type and its endpoints, and derive something from them. This derivation will introduce us to the machinery that powers much of Servant’s functionality.

A large fraction of software engineers work in web development.

I also do some web development these days, exclusively on the backend. Backend software engineers, just like their frontend counterparts, have streamlined their work by packaging development utilities into frameworks. Even in the relatively small Haskell community, there are many web frameworks, ranging from quick-to-start (scotty) to fully-featured-and-opinionated (Yesod and IHP).

The Haskell community has historically been fertile ground for innovation; web development is no different. One framework in particular has pushed the boundary of what it means to write web applications: Servant. Don’t be fooled by the deceptively simplistic website: Servant is one of the crown jewels of the Haskell ecosystem. It combines the broad appeal of writing web applications, with the use of some of Haskell’s most advanced type system features to perform incredible feats of engineering.

Servant is worth discussing and studying for two reasons.

The first is to use Servant as a concrete application of type-level computation. In this respect, I hope readers can take some of the design ideas from Servant and bring it back to their community, just like QuickCheck pioneered property-based testing. The second is that while Servant is powerful, it remains a rather sophisticated piece of software that is hard to learn and understand. Even with some Haskell experience, Servant is not yet a pick-up-and-go tool; wandering off the beaten path (i.e. doing anything not covered in the documentation) remains a daunting prospect for many, as it was for me. By studying the inner workings of Servant, we can learn about how to use it, and extend it, effectively.

I want to celebrate the boldness of Servant, while teaching you about its ways. This is why I am starting a blog series, where I will cover the basics of Servant by implementing a simple version of Servant’s internals, as literate Haskell files. By constructing Servant, we will both learn various techniques involving Haskell’s advanced type system, but also demystify the real Servant library.

This blog series will build in complexity. We will start by representing an API as a type. This type won’t be useful straight away, but subsequent blog posts will showcase one capability of Servant by using this type, starting with generating type-safe links to endpoints, and culminating with automatically generating clients of APIs.

Blog posts in this series

• An API as a type
• Type-safe links
• Serving an API
• Automatic derivation of client functions

Update

This is the end of the planned posts in the Servant by construction series. If there’s another Servant-related topic you’d like to learn more about, by having me build a simplified version, don’t hesitate to reach out!

The Haskell Foundation is driven by a vision. Haskell has a rich history of academic research, innovation, and industry usage driven by strong principles. Within this vision, I personally want focus on boosting the community’s health on two fronts.

The first front is industry adoption. I took a new Haskell-focused role this year, and Haskell’s unique strengths – as well as unique challenges – are front-of-mind. The Haskell Foundation is ramping up efforts to spend resources on its technical agenda. If you use, or plan to use, Haskell in production, we would love to hear how we can help you (contact info at the end of this post).

The second front is the successful conversion of Haskell curiousity to Haskell knowledge, especially amongst experienced programmers. Over the years, I have spoken with many, many people whose curiosity, although intense, did not materialize into knowledge of Haskell. My own experience of learning and using Haskell was, and remains, a wonderful intellectual journey, and I want everyone to be able to experience the same thing. I’ll have more to say about how we plan to tackle this in the next few months.

If any of these two challenges are of interest to you, do not hesitate to reach out to me at my new email (laurent@haskell.foundation).

I am a firm believer in the purely functional programming approach, embodied by the Haskell programming language. While the Haskell community is not huge, it is large enough that I can work on most domains.

Most domains, but not all; data science remains hard to work on in Haskell. Since data science grew out not from software engineering, but from students and scientists, the best data science tools are found in other communities such as R and Python. If we focus further on machine-learning and “““AI”“” (ಠ_ಠ), then the distribution of high-quality tools is even more concentrated in the Python community.

I have started exploring what it would look like to build a Haskell-centric data science workflow more than a year ago, with the implementation of a Series data structure. While this was perfect for my use-case at the time (I wrote about it here and here), the typical data scientist is used to columnar the data structure known as the dataframe.

Recently, an effort to design a dataframe interface in Haskell has been spearheaded by Michael Chavinda, with a focus on exploratory data science. This effort trades type safety for easier interactivity, similar to Python’s pandas DataFrames.

In this blog post, I want to explore a different design tradeoff: what if one were to instead focus on type-safe expressiveness, with no regards to interactivity? What would such a dataframe interface look like?

The design below is based on some intermediate type-level shenanigans. I was inspired by the approach that the Beam SQL project took, based on higher-kinded types.

Let’s get imports out of the way:

{-# LANGUAGE DefaultSignatures #-}
{-# LANGUAGE DeriveGeneric #-}
{-# LANGUAGE TypeFamilies #-}

module HKTGenerics where

-- from `base`
import Data.Functor.Identity (Identity(..))
import Data.Kind (Type)
import GHC.Generics

-- from `vector`
import Data.Vector (Vector)
import qualified Data.Vector

Let’s consider an example: we want to represent a set of people of some sort. We would normally represent one person using a record type like so:

data SimpleUser
    = MkSimpleUser { simpleUserFirstName :: String
                   , simpleUserLastName  :: String
                   , simpleUserAge       :: Int
                   }

Now, a dataframe of such users should be equivalent to:

data FrameUser
    = MkFrameUser { frameUserFirstName :: Vector String
                  , frameUserLastName  :: Vector String
                  , frameUserAge       :: Vector Int
                  }

where each record is a Vector (similar to arrays in other languages), representing a column. This is the main draw of dataframes: data is stored in columns, rather than simply e.g. Vector SimpleUser. This is not always best, but I will assume that the user has knowledge of the tradeoffs.

The structures of SimpleUser and FrameUser are extremely similar. We can use higher-kinded types to unify them by introducing a type parameter f which represents the container for values:

data HKTUser f
    = MkHKTUser { hktUserFirstName :: f String
                , hktUserLastName  :: f String
                , hktUserAge       :: f Int
                }

Here, f has type f :: Type -> Type, just like the Vector type constructor. HKTUser is called a higher-kinded type, because unlike a type like SimpleUser, which has kind Type, HKTUser isn’t a type, but a type constructor. I won’t go into more detail than this on higher-kinded types; consider watching the Haskell Unfolder episode on the subject.

Using this method of representing users, we can represent SimpleUser as HKTUser Identity, and FrameUser as HKTUser Vector. Here, Identity is the trivial container.

One more thing before we move on. While Identity is a trivial functor, it still adds some overhead; HKTUser Identity and SimpleUser aren’t exactly equivalent. We can optimize this overhead away using a type family:

type family Column (f :: Type -> Type) x where
    Column Identity x = x -- Optimization

    Column Vector x = Vector x

Finally, we can unify the representations of SimpleUser and FrameUser:

data User f
    = MkUser { userFirstName :: Column f String
             , userLastName  :: Column f String
             , userAge       :: Column f Int
             }

The Column type family can be thought of a type-level function: Column f a is a type that depends on f. To be clearer, let’s create type synonyms:

type Row   (dt :: (Type -> Type) -> Type) = dt Identity
type Frame (dt :: (Type -> Type) -> Type) = dt Vector

Using these synonyms, Row User is equivalent to SimpleUser. while Frame User is equivalent to FrameUser. We can operate on the columns of dataframes easily, like so:

-- | Returns the longest first name out of a dataframe of users.
-- If the dataframe is empty, returns the empty string.
longestFirstName :: Frame User -> String
longestFirstName = Data.Vector.foldl' longest mempty . userFirstName
    where
        longest :: String -> String -> String
        longest x y = if length x >= length y then x else y

With longestFirstName, we can glimpse the performance advantage of using dataframes: the userFirstName field is really an array, and so finding the longest first name is an operation on an array of string rather than an array of User.

How can we build a dataframe? We can turn rows of, well, Row User into a single Frame User like so:

buildUserFrame :: Vector (Row User) -> Frame User
buildUserFrame vs
    = MkUser { userFirstName = Data.Vector.map userFirstName vs
             , userLastName  = Data.Vector.map userLastName vs
             , userAge       = Data.Vector.map userAge vs
             }

This is a little tedious; for every type of dataframe, we need to write our own dataframe construction function! Can we write a function like Vector (Row t) -> Frame t, which works for any t? Yes we can.

Enter generics

I want to thank Li-yao Xia (Lysxia on the Haskell Discourse) for helping me figure out how to do what you’re about to read!

If you squint, every type we would want to turn into a dataframe has the same structure: a record type where every record is either Vector a or Identity a (nesting dataframes is out of scope for today). We can provide functionality for any suitable record type like that using Haskell generics¹.

In Haskell, the Generic typeclass has nothing to do with “generics” in other programming language. “Generic” programming in Haskell is done with ad-hoc polymorphism (i.e. typeclasses). Instead, the Generic typeclass in Haskell is used to transform any datatype t into a generic representation, called Rep t, which can be used define functions which work over a large class of types. Specifically, in our case, we want to create a function Vector (Row t) -> Frame t which works for any higher-kinded record type t like User.

There are many explanations of Haskell’s Generic, such as Mark Karpov’s Generics explained blog post. The wrinkle in our dataframe problem is that types such as User are higher-kinded, and therefore some more care is required.

Let’s define our problem. We want to create a typeclass FromRows with a method, fromRows:

class FromRows t where
    fromRows :: Vector (Row t) -> Frame t

We also want to provide a default definition of fromRows such that downstream users don’t have to manually write instances of FromRows:

    default fromRows :: (???) => Vector (Row t) -> Frame t
    fromRows = ???

How can we write the default implementation of fromRows?

The key concept to remember is that Generic only works with types of kind Type, i.e. Row User but not User. For every higher-kinded type t (like User), we care about two concrete types: Row t and Frame t. Therefore, we need to index our typeclass on both concrete types at once.

Enough word salad:

class GFromRows r -- intended to be `Row`-like
                f -- intended to be `Frame`-like
    where
    gfromRows :: Vector (r a) -> (f a)

We need to provide instances relating to some (but not all) generic constructs, including M1 (which is always required), K1, and (:*:).

We start with the generic metadata type, M1:

instance GFromRows r f => GFromRows (M1 i c r) (M1 i c f) where
    gfromRows :: Vector (M1 i c r a) -> M1 i c f a
    gfromRows = M1 . gfromRows . Data.Vector.map unM1

Then move on to :*::

instance ( GFromRows r1 f1
         , GFromRows r2 f2
         )
         => GFromRows (r1 :*: r2) (f1 :*: f2) where
    gfromRows vs = let (xs, ys) = Data.Vector.unzip
                                $ Data.Vector.map (\(x :*: y) -> (x, y)) vs
                    in gfromRows xs :*: gfromRows ys

Finally, onto the representation of fields of constructors, K1:

instance GFromRows (K1 i r) (K1 i f) where
    gfromRows = K1 . Data.Vector.map unK1

Note that the above will not compile. For the instances of M1 and :*:, we assumed that r and f already had an instance of GFromRows. In the instance for K1, the compiler does not know about the relationship between r and f yet. In some sense, the instance involving the representation K1 is the foundation on which other instances are defined.

We can refine our instance by enforcing that f be an array of r using (f ~ Vector r):

instance (f ~ Vector r) => GFromRows (K1 i r) (K1 i f) where
    gfromRows :: Vector (K1 i r a) -> K1 i f a
    gfromRows = K1 . Data.Vector.map unK1

We can now fill in the default implementation of fromRows:

class FromRows t where
    fromRows :: Vector (Row t) -> Frame t

    default fromRows :: ( Generic (Row t)
                        , Generic (Frame t)
                        , GFromRows (Rep (Row t)) (Rep (Frame t))
                        )
                     => Vector (Row t)
                     -> Frame t
    fromRows = to                   -- Turn `Rep (Frame t)` back into `Frame t`
             . gfromRows            -- Vector (Rep (Row t)) -> Rep (Frame t)
             . Data.Vector.map from -- Turn every row into a `Reo (Row t)`

How can we use this? Behold:

data User f
    = MkUser { userFirstName :: Column f String
             , userLastName  :: Column f String
             , userAge       :: Column f Int
             }
    deriving (Generic) -- This is new

What’s new here is that we need to derive a Generic instance for User. Then, the instance of FromRows User requires no method implementation:

instance FromRows User

Then, we can re-implement buildUserFrame trivially:

buildUserFrame :: Vector (Row User) -> Frame User
buildUserFrame = fromRows

Further work: nesting dataframes

The implementation above works, but we assumed that every record type had fields of the form Column f a. How about nesting dataframes types? Consider this:

data Address f
    = MkAddress { addressCivicNumber :: Column f Int
                , addressStreetName  :: Column f String
                }
    deriving (Generic)

instance FromRows Address

data Store f
    = MkStore { storeName    :: Column f String
              , storeAddress :: Address f
              }
    deriving (Generic)

instance FromRows Store -- type error

Ideally, we would want this Store type above to be equivalent to:

data Store f
    = MkStore { storeName          :: Column f String
              -- Address gets unpacked into "adjacent" columns
              , addressCivicNumber :: Column f Int
              , addressStreetName  :: Column f String
              }
    deriving (Generic)

I haven’t figured out how to do this yet, but it would be desirable.

This document is a literate Haskell module!

Until the end of undergraduate school, this was mostly done by hand. Optimizing the trajectory of a heavy ball or solving the heat equation are problems with analytical solutions, and thus can be solved with pen(cil) and paper.

However, there were instances when numerical tools had to be used, rather than analytical ones. This occurred, for example, when replacing models of the physical world with measurements from the physical world in experimental physics classes. By the end of my B.Sc., the need to take measurements, transform them, and report results was made much simpler by using a computer.

Fast forward to graduate school, and the amount of measurements (and their complexity) require the use of some of the most powerful computers I have ever used, even to this day. When implementing numerical routines, I had to pore over the equations (translated to computer expression) countless times, to ensure that they were correctly applied. Most importantly, all units needed to be carefully checked by hand. Small mistakes went unnoticed and wasted valuable resources. Take a look at one of the computations from my Ph. D. dissertation (PDF, Git repository):

from scipy.constants import physical_constants

def population(temperature: float, frequency: float) -> float:
    """
    Determine average phonon population at `temperature`.

    Parameters
    ----------
    temperature : float
        Temperature in Kelvin
    frequency : float
        Phonon frequency in Hertz
    """
    h, *_ = physical_constants["Planck constant over 2 pi in eV s"]
    kb, *_ = physical_constants["Boltzmann constant in eV/K"]
    return 0.5 * coth(h * frequency / (2 * kb * temperature)) - 0.5

This isn’t a complex equation, but it showcases the problem perfectly. temperature, frequency, h, and kb are all floating-point numbers, with their units attached as documentation. This is not robust.

These days, instead of meticulously going over the details of calculations ahead of time, I now defer to my computer to check the validity of my calculations as much as possible. That’s why computers exist: to free people from repetitive and error-prone work. In this post, I will describe a mechanism, typed dimensions, by which we can eliminate entire classes of bugs, and how the dimensional Haskell package makes this easy.

Dimensions, units, and quantities

In the international system of units (also called SI units), there are 7 basic dimensions a physical value can have:

• time duration $T$;
• length $L$;
• mass $M$;
• electric current $I$;
• thermodynamic temperature $\Theta$;
• amount of substance $N$;
• luminous intensity $J$.

Using the symbols associated with these base dimensions, we can express any dimension using exponents. For example, velocity (length over time duration) has dimensions $L/T = L \cdot T^{-1}$, while force (mass-length over time squared) has dimensions $M \cdot L \cdot T^{-2}$. Dimensionless quantities have all exponents being 0.

Why are dimensions important? There are mathematical rules associated with combining numbers with dimensions:

• Two quantities with dimensions $D_1$ and $D_2$ can only be added or subtracted if $D_1 \equiv D_2$. For example, it does not make sense to add a length to a mass¹.

• Any two quantities with dimensions $D_1$ and $D_2$ can be multiplied or divided, in which case the resulting dimension follows the usual rules of arithmetic. For example:

$$\begin{align} \left( L \cdot T^{-1} \right) / \left( L \cdot \Theta\right) &= \left( L \cdot T^{-1} \right) \cdot \left( L^{-1} \cdot \Theta^{-1}\right) \\ &= L^{1 - 1} \cdot T^{-1} \cdot \Theta^{-1} \\ &= T^{-1} \cdot \Theta^{-1} \end{align}$$

From these two facts, we can derive some surprising conclusions. For example, the argument to many functions (such as sine, cosine, exponential, etc.) must be dimensionless! Consider the Taylor series expansion of the sine function:

$$\sin{x} = x - \frac{x^3}{3!} + \frac{x^5}{5!} - ...$$

The argument $x$ must have the same dimensions as $x^3$, which is only possible if and only if $x$ is a dimensionless quantity.

Units of measure are physical manifestations of dimensions. Dimensions are abstract, while units of measure are concrete. For example, the length dimension $L$ can be measured in units of meters. Each basic dimension has its own canonical unit of measure, the base unit:

• The second (s) for time duration $T$;
• The meter (m) for length $L$;
• The kilogram (kg) for mass $M$;
• The ampere (A) for electric current $I$;
• The kelvin (K) for thermodynamic temperature $\Theta$;
• The mole (mol) for amount of substance $N$;
• The candela (cd) for luminous intensity $J$.

Units for non-basic dimensions, so-called derived units, are combinations of base units using the usual multiplication ($\cdot$) and division ($/$) operators. For example, velocity has dimensions of $L \cdot T^{-1}$, and can be measured in units of meters per second ($\frac{m}{s}$). Some derived units have names; for example, the Newton (N) is a derived unit corresponding to $\frac{\text{kg} \cdot \text{m}}{\text{s}^2}$.

Based on their dimensions, units can only be combined in certain ways. You can only add/subtract units of the same dimensions, while the multiplication/division of units modifies the dimensions.

Units can be converted to any other units of the same dimensions by conversion base unit. For example, converting from units of imperial feet (ft) to kilometers (km) involves conversion from imperial feet to the base unit of length, the meter, and then conversion from the meter to the kilometer.

Finally, a quantity is a number attached to units. 3.15 meter/second is a quantity with magnitude 3.15, units of meters/second, and dimensions of length over time duration (or $L \cdot T^{-1}$).

Scientists take measurements of quantities, and run scientific computations to get answers in the form of other quantities. We can ensure correctness of these computations by realizing that dimensions are known ahead of time. This means that for statically- and strongly-typed languages (e.g. Haskell, Rust), we should enforce correctness using the type system.

Type-safe dimensions

People’s first contact with computational unit systems may come from pint, a Python library to manipulate quantities. While pint is better than nothing, it does not guarantee correctness at runtime due to Python’s dynamic nature.

Instead, I prefer the dimensional package, a Haskell library created by Björn Buckwalter that guarantees correctness by ensuring type-safe dimensions at compile-time. Other tools exist for other languages – for example, F# famously includes units of measure as a first-party feature.

We will work by example to compute the Maxwell-Boltzmann distribution. This is the distribution of velocities of identical particles of mass $m$, given some thermodynamic temperature $T$:

$$f(v) = \left( \frac{m}{2 \pi k_B T}\right)^{\frac{3}{2}} \exp{ \left( -\frac{m v^2 }{2 k_B T}\right) }$$

where $v$ is the magnitude of particle velocity in a three-dimensional space, and $k_B$ is the Boltzmann constant.

Without typed dimensions, the computation of this distribution can be done as follows:

-- Boltzmann constant in Joules/Kelvin
boltzmannConstant_JpK :: Double
boltzmannConstant_JpK = 1.380649e-23


untypedMaxwellBoltzmannDist :: Double -- ^ Particle mass in kilogram
                            -> Double -- ^ Thermodynamic temperature in Kelvin
                            -> Double -- ^ Particle velocity in meters/second
                            -> Double -- ^ Probability density (dimensionless)
untypedMaxwellBoltzmannDist mass_kg temp_K velocity_mps 
    = ( mass_kg / (2 * pi * boltzmannConstant_JpK * temp_K) ) ** (3/2) 
    * exp ( - (mass_kg * velocity_mps **2) / (2 * pi * boltzmannConstant_JpK * temp_K) )

It’s not too hard to check units by hand – but it is tedious and error-prone.

Now let’s do this again, using dimensional.

Setup: I am using the GHC2024 language edition. We will also replace the (implicitly imported) Prelude module to use Numeric.Units.Dimensional.Prelude, which replaces the usual arithmetic operators to use dimension-aware ones, as well as importing the Unit, Dimension, and Quantity types.

{-# LANGUAGE NoImplicitPrelude #-}

import Numeric.Units.Dimensional.Prelude

To get acquainted, let’s convert the definition of the Boltzmann constant. The dimensions of the Boltzmann constant are called DHeatCapacity in dimensional. Therefore, we can write:

boltzmannConstant :: Quantity DHeatCapacity Double

which means that boltzmannConstant is a Quantity of dimension DHeatCapacity, whose magnitude is represented by a Double. We use the (*~) operator to combine a number (1.380649e-23) with a compound unit, joule / kelvin, to get:

boltzmannConstant :: Quantity DHeatCapacity Double
boltzmannConstant = 1.380649e-23 *~ (joule / kelvin)

We are not yet ready to implement the Maxwell-Boltzmann distribution function. One particular wrinkle is that exponents (such as the $3/2$ exponent of the first term) change the dimensions (i.e. the type) of the input. Therefore, some type arithmetic is required. To this end, dimensional provides (^) to raise to an integer power, and sqrt to take the square root, while appropriately changing the dimensions at compile time. The type signatures are non-trivial to say the least, as it involves compile-time manipulation of types. The operation of “raising to the three-halfs power” becomes:

raiseToThreeHalfsPower :: Floating a 
                       => Quantity d a 
                       -> Quantity (NRoot d Pos2 ^ Pos3) a
raiseToThreeHalfsPower x = (sqrt x) ^ pos3

where pos3 is a type-level integer. The dimension (NRoot d Pos2 ^ Pos3) will resolve to the appropriate dimension at compile-time via type families once d is known.

Finally, we can implement the (dimensionally-typed) Maxwell-Boltzmann function:

maxwellBoltzmannDist :: Mass Double
                     -> ThermodynamicTemperature Double
                     -> Velocity Double
                     -> Dimensionless Double
maxwellBoltzmannDist mass temp velocity 
    = raiseToThreeHalfsPower ( mass / (_2 * pi * boltzmannConstant * temp) )
    * exp ( negate (mass * velocity ^ pos2) / (_2 * pi * boltzmannConstant * temp) )

where _2 is the dimensionless integer 2, and (*), (/), exp, negate, and ^ are all dimensionally-aware operators from dimensional (rather than the Prelude module).

If you compile the program above, you’ll get an error message ಠ_ಠ:

Couldn't match type ‘Neg3’ with ‘Zero’
  Expected: Dimensionless Double
    Actual: Quantity 
                (NRoot 
                    (DMass 
                        / ((Dim Zero Zero Zero Zero Zero Zero Zero * DHeatCapacity) * DThermodynamicTemperature)) 
                    Pos2 ^ Pos3
                ) 
                Double
(...snip...)

This is because I’m a sloppy physicist – sorry! The Maxwell-Boltzmann distribution is not a dimensionless quantity: it actually returns a velocity density with dimensions of $1 / (L^3 \cdot T^{-3})$, or $L^{-3} \cdot T^{3}$.

Let’s fix this. There is no type synonym for velocity density in dimensional, but we can create one ourselves.

type DVelocityCube = DVelocity ^ Pos3

type DVelocityDensity = Recip DVelocityCube -- dimension
type VelocityDensity = Quantity DVelocityDensity -- quantity

Our final version of maxwellBoltzmannDist becomes:

maxwellBoltzmannDist :: Mass Double
                     -> ThermodynamicTemperature Double
                     -> Velocity Double
                     -> VelocityDensity Double
maxwellBoltzmannDist mass temp velocity 
    = raiseToThreeHalfsPower ( mass / (_2 * pi * boltzmannConstant * temp) )
    * exp ( negate (mass * velocity ^ pos2) / (_2 * pi * boltzmannConstant * temp) )

We can compute the result of maxwellBoltzmannDist in any compatible unit. We will do this for a gas of diatomic nitrogen. In an interactive Haskell session:

ghci> import Numeric.Units.Dimensional.NonSI ( unifiedAtomicMassUnit ) -- unifiedAtomicMassUnit = amu
ghci>
ghci> let n2_mass          = 2     *~ unifiedAtomicMassUnit
ghci> let room_temperature = 300.0 *~ kelvin
ghci> let velocity         = 400   *~ (meter / second)
ghci>
ghci> maxwellBoltzmannDist n2_mass room_temperature velocity 
4.466578950309018e-11 m^-3 s^3

We can easily request specific output units using the (/~) operator. In this case, we convert result to (hour / nautical mile)³:

ghci> import Numeric.Units.Dimensional.NonSI ( nauticalMile, degreeRankine, knot )
ghci>
ghci> let n2_mass          = 2.6605E-27 *~ kilo gram
ghci> let room_temperature = 491.0      *~ degreeRankine
ghci> let velocity         = 777        *~ knot
ghci>
ghci> (maxwellBoltzmannDist n2_mass room_temperature velocity) /~ ((hour / nauticalMile) ^ pos3)
5.041390507268275e-12

Design and tradeoffs

This section was added on Nov. 24th, 2024 following discussions on Hacker News and the Haskell Discourse

There are many other software packages that support some level of type-safe computational unit systems such as mp-units for C++, Physics::Measure and Physics::Unit for Raku, Unitful for Julia, Physical for Swift, and more. There’s even an entire programming language designed around it called Numbat. So what can we learn from dimensional’s design, and importantly, its tradeoffs?

Beyond checking to inference of dimensions

One key feature of dimensional is that it does not only check validity, but also infers the dimensions of expressions at compile-time. Take for example, consider the question “What is the type (:t) of 1 meter divided by 1 second?”:

ghci> :t (1 *~ meter) / (1 *~ second)
Quantity (Dim Pos1 Zero Neg1 Zero Zero Zero Zero) Double

If you read the documentation for Dimension, you will notice that (Dim Pos1 Zero Neg1 Zero Zero Zero Zero) is the dimension of velocity (also known as DVelocity).

This means that the compiler becomes a helpful assistant, rather than simply telling you when you are wrong.

Compile-time dimensions, runtime units

Another key design of dimensional is that the dimensions are typed, but units are runtime values. This has important advantage, but also one major drawback.

The important advantage is flexibility: programs written using dimensional accept a wide variety of inputs whose dimensions are equivalent. Since values’ dimensions are known at compile-time, we can be guaranteed that values will be convertible to base units at runtime. You can see this in the usage of maxwellBoltzmannDist above, where I varied the input units without issues, even mixing SI units like kelvin and non-SI units like degreeRankine.

This flexibility comes with a performance cost: each quantity is now composed of two values, the magnitude and the unit, which means that that mathematical operations will be slower. For performance-sensitive code, I recommend validating inputs using dimensional, and converting to raw Double using (/~) before compute-heavy operations.

Non-extensibility

dimensional is limited to the 7 physical dimensions by design. However, other libraries such as units, allow the creation of extensible unit systems, not limited to physical dimensions.

The lack of extensibility is not an inherent design choice, but rather an implementation choice. This may change in the future.

Conclusion

This was a whirlwind tour of dimensional with a practical example. If this was your first introduction to typed dimensions in Haskell, do not be alarmed – I bounced off of it the first time.

As mentioned, software design is about trade-off. Using dimensional is complex, but it isn’t complicated²; it makes you address the complexity of dimensions and units up-front, rather than hoping for the best. Sometimes this doesn’t make sense, but for critical calculations, there is nothing like typed dimensions.

I am now a maintainer of dimensional on GitHub, and I want nothing more than to help people use typed dimensions (when it makes sense). If you have any feedback, for example missing features or lacking documentation, feel free to raise an issue!

Code available in Haskell module.

Starting a business is something that I have been thinking about since finishing graduate school. My academic expertise could not be turned into a business outright (although ex-colleagues are trying!), but my skills in mathematics, software engineering, and computer science have a broader applicability.

Mathilde and I want to act on the climate emergency. As simple citizens, our actions have a limited effect. However, by starting the right business, we can create a movement which has a tangible impact. I am positively inclined towards technology startups specifically because of the growth curve. This means that if everything goes right, Powerweave could change the world.

For many reasons, including the push towards sustainable energy and the increasing demand for energy due to a resurgence of artificial intelligence progress, power grid infrastructure is under tremendous stress, and technologies are evolving rapidly to address this. The space is fertile ground for innovators that seek to help the world in a concrete way. In order to get both startup and industry experience, I joined SocïVolta, a technology startup that operates at the intersection of financial markets and the North American power grid. This is also where I met Mathilde. We both gained invaluable insights into how the North American power infrastructure works – and where its weaknesses are.

In this post, I will describe current power infrastructure, how Powerweave helps, and what’s next for us.

What is the North American power grid?

The power grid is an electrical network which can be categorized into three broad levels:

• Generation: power stations, which are often far from population centers;
• Transmission: long-distance electrical transmission lines connecting power stations to population centers;
• Distribution: network of low-voltage transmission to homes and businesses.

There are places in North America where all three levels are controlled by a single entity (e.g. Hydro-Québec). But increasingly, different entities own and operate different levels of the power grid.

What is the provenance of the electricity that powers your screen right now? It might not be from the closest power station. The provenance of your electricity depends on lots of factors, including who else wants electricity right now, and who is currently generating electricity. Sometimes, it is better to use a power source far from you, but that takes a path which is relatively unused.

Most people want cheap electricity. Getting you the cheapest power every second of the year requires coordination between all operating entities on the power grid. The modern way to coordinate the behavior of the power grid at all levels are so-called wholesale electricity markets. At wholesale electricity markets, power station owners, transmission line owners, and energy service providers come together to enter auctions to determine the geographical price of electricity. While the details of such auctions are far beyond the scope of this blog post, the important bit is that power auctions answer the following two questions:

1. Where does the energy produced by a power station get consumed?
2. What is the cost of this energy at every node in the power grid?

Wholesale electricity markets have been shown to increase competition and lower electricity rates, as well as integrate renewable energy resources more effectively. That is why you see them popping up more and more across the world. The European Union even codified it into law in 2019.

Local electricity distribution

Let’s zoom in on the last level, where Powerweave operates: local electricity distribution.

It used to be that local distribution of electricity was squarely in one direction: homes and businesses would only consume electricity. With the advent of rooftop solar panels and home batteries, this is no longer true. Homes and businesses can act as spontaneous, small power stations called distributed energy resources.

On one hand, we should encourage individuals and businesses to produce their own energy and even export it back to the grid at certain times. Electricity consumption per capita is increasing rapidly, which is stressing power infrastructure. Individuals and businesses that produce and consume energy, prosumers, invest in power infrastructure so that the utilities don’t have to – a concept known as virtual infrastructure upgrades. The alternative is that energy service providers (e.g. utilities) invest in infrastructure, in which case all rate-payers split the bill.

On the other hand, energy service providers are either not ready, or unwilling, to absorb spontaneous extra energy from prosumers. From an electricity distributor point-of-view, it would be much better for electricity to be consumed close to where it is generated (community self-consumption).

At the local distribution level, what is now needed is coordination between all rate-payers in a community. Does this problem remind you of something?

So what is Powerweave?

Powerweave operates a platform that coordinates all rate-payers in a community. It solves the problem of incentivizing rate-payers to invest in power infrastructure and to be more energy efficient when the power grid needs it the most, while also ensuring community self-consumption.

The Powerweave platform is centered around local power auctions, or local electricity markets. For each community, auctions are conducted at regular intervals (usually 5 minutes). Just like wholesale power markets, each auction covers a period of electricity consumption/generation in the near future:

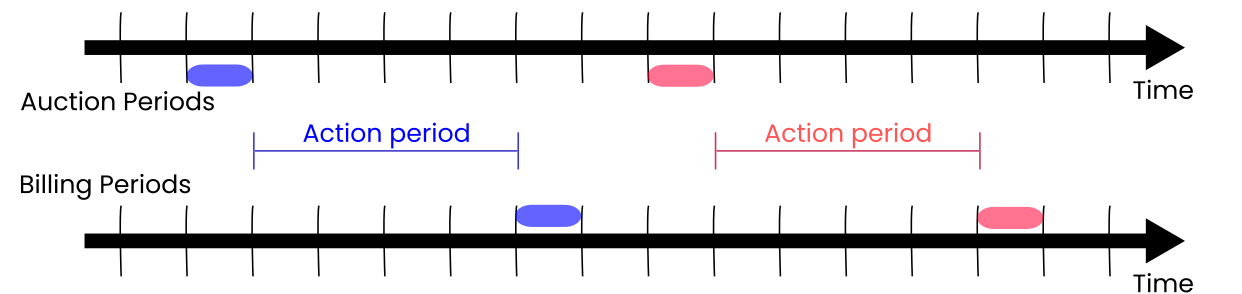
The time between an auction ending, and its corresponding billing period starting, is the action period. This is a period during which rate-payers know how much power will cost, but they still have influence over how much power they consume or generate.

I cannot stress enough how the existence of the action period is key to Powerweave. Consider this example.

I am charging my electric car, which will require quite a bit of power (10kW) over the next 8 hours. I participate in the next power auction, where I bid for 10kW of power. However, when closing the auction, I am only cleared to draw 4kW of solar power from a few neighbors at a reasonable price; the shortfall (6kW) will be covered by my utility at a higher price, since the grid is under stress right now. Knowing this in advance, I can slow down or pause charging my vehicle until I can get a better overall energy price.

This example is the foundation of Powerweave. As a rate-payer, I minimized my electricity bill and used clean sustainable power. My utility incentivized me to be more energy efficient when it mattered, and it also saved on infrastructure costs. Win-win!

However, as you can imagine, constantly participating in auctions and adjusting power consumption/generation (day and night!) is unrealistic for most people. Therefore, Powerweave automates all of this.

On the auction side, Powerweave can trade on behalf of rate-payers. Using statistical and machine-learning models trained on historical consumption and generation data, as well as external data such as weather forecasts, Powerweave can place bids and offers for power to achieve goals set by each rate-payer, such as minimizing energy costs, or minimizing carbon emissions. These models are tireless and self-adjusting; you never need to participate in auctions directly if you don’t want to.

On the pricing response side, Powerweave integrates with third-parties (e.g. smartphone notifications, electric vehicle charging systems, smart thermostats) to automatically adjust your load or generation profile.

Our technology is unique in North America (although related technologies have been trialed in the past). Powerweave can legally operate in about 10 US states (including New York and California), with more states potentially opening up soon. Powerweave probably could not have operated even just 5 years ago. We exist at the edge of regulations; this is a great opportunity to influence US-wide reforms on local energy coordination.

The near future

Mathilde and I have completed an early technology demonstration, to show that Powerweave’s offering can indeed be realized. We are using a lot of cool technology, which I hope to share with you soon!

Right now, we are focused on partnering with one energy service provider (utility, community choice aggregation, or independent microgrid) to run a pilot project. This will demonstrate that our technology is beneficial, and give confidence to less-technologically-inclined energy service providers (which are most of them) that Powerweave can help them.

If you can help us connect with decision makers at energy service providers, I would love to hear from you. Getting the first contact with potential partners is difficult; being introduced by someone else helps tremendously.

We hope to grow the team soon as well. If you are interested in Powerweave’s mission, be sure to follow us on LinkedIn!

This year, my employer is expanding its trading operations to a new class of products. Since there is no overlap between this new work and our current operations, I got to design a technology stack most suited for the task. This technology stack includes Haskell, most importantly because wrong or unexpected trading decisions can (and have) cost us dearly.

In this blog post, I want to show you the basics of how we designed the framework in which to express trading strategies.

The fundamentals of trading strategies

The fundamental pieces of trading operations are strategies. In algorithmic trading, strategies are computer programs that decide what to trade, and how to trade it, at any given moment.

Let’s take the example of a simple trading strategy that is only concerned with AAPL stock. The current stock price is about 190 USD today; our example strategy is defined thusly:

• If the AAPL price rises above 200, sell our holdings (if we have any);
• If the AAPL price falls below 180, buy 10 shares;

In this case, the result of this strategy is some signal to buy or sell AAPL stock. We can run our strategy in a loop:

import qualified Control.Monad

data Action = Buy Int
            | Sell
            | Hold

type Price = Double

main :: IO ()
main = Control.Monad.forever $ do
    aaplPrice <- fetchMostRecentPrice
    let action = myStrategy aaplPrice
    executeMarketAction action
    where
        myStrategy :: Price -> Action
        myStrategy aapl_price
            | aapl_price > 200 = Sell
            | aapl_price < 180 = Buy 10
            | otherwise        = Hold

        fetchMostRecentPrice :: IO Price
        fetchMostRecentPrice = (...)

        executeMarketAction :: Action -> IO ()
        execureMarketAction = (...)

and boom, you have a simple trading system!

Once you have a good idea for a strategy, you should test it on historical data. This is called backtesting. Backtesting strategies is, by definition, much more computationally intensive than live trading, since you are evaluating your strategy on much more data. We often backtest strategies on 5-10 years’ worth of data when it makes sense, and sometimes more.

I will also note that it is easiest to have strategies that can run in various contexts (including backtesting and live operations) if the strategy is pure (in the mathematical sense). It is in the quest for purity and performance that we decided to implement the trading system for a new asset class in Haskell.

Trading strategies in Haskell

For the simplicity of presentation, we will only consider strategies that involve prices. The simplest such strategies are strategies which depend on the most recent price:

newtype Strategy
    = MkStrategy { runStrategy :: Price -> Action }

Strategy is a type of functions, from the most recent Price known to some market action. This is only re-packaging the example above.

Let’s build a backtesting framework. There are two parts here:

• determine historical market actions;
• simulate the effects of market actions.

In practice, the two parts of backtesting are handled simultaneously. However, for simplicity, I will only consider the first part here.

The nature of this problem is well-suited to streaming approaches; I will use pipes¹:

-- From the `time` package
import           Data.Time     ( UTCTime )
-- From the `pipes` package
import           Pipes         ( Producer, (>->) )
import qualified Pipes
import qualified Pipes.Prelude as Pipes

-- | From a stream of input features, produce a stream
-- of output 'Market' actions
backtestStrategy :: Monad m
                 => Strategy r
                 -> Producer (UTCTime, Price)  m () -- ^ stream of timestamped AAPL prices
                 -> m BacktestResults
backtestStrategy strat prices
    =   prices
    >-> Pipes.map (\(k, f) -> (k, runStrategy strat f))
    >-> simulateMarketActions

-- The following is out-of-scope

data BacktestResults = MkBacktestResults (...)

simulateMarketActions :: Consumer (UTCTime, Action) m BacktestResults
simulateMarketActions = (...)

More expressive strategies

I have a problem with the above definition of Strategy: I’m limited to strategies based on the single, most recent Price. What if I had a good idea for a strategy which involves the last 10 price values? Our Strategy type is not expressive enough: it only takes one type of feature, while we want to support a wide range of features.

I will define a Strategy type which removes restrictions on the input feature:

newtype Strategy r
    = MkStrategy { runStrategy :: r -> Action }

with the understanding that the data of type r is somehow derived from prices.

What are some features derived from prices, that we might be interested in?

• Price history, e.g. most recent N ticks;
• Price aggregations, e.g. average of most recent M ticks;
• Rolling aggregations, e.g. N-tick history of the averages of M ticks;

Every conceptual feature described above has some free parameters. We don’t want to have separate strategies like Strategy PriceHistoryForPast10Ticks and Strategy PriceHistoryForPast20Ticks. More specifically, for every feature of type r, there is a type of parameters p which describes the parameters of r.

For example²:

-- from the `javelin` package
import Data.Series ( Series )

-- Feature I may want to use in a strategy
newtype PriceHistory
    = MkPriceHistory (Series UTCTime Price)

-- Parameters that may affect the featyre `PriceHistory`
data NumTicks
    = MkNumTicks { numTicks :: Int }

Typed features and their parametrization

We could list all possible features in a big sum type:

data Feature
    = FPrice Price
    | FPriceHistory (Series UTCTime Price)
    | FAveragePrice Price
    | (...)

However, it’s rather cumbersome to create a strategy to experiment with new features. We can do better.

We want to be able to link the types PriceHistory and NumTicks such that they are used together when backtesting, to ensure type safety. This is the domain of indexed type families, or type families for short. We will amend our Feature type to become a typeclass, and upgrade backtestStrategy function to take into account feature parametrization:

class Feature r where
    -- For every instance `r` of `Feature`,
    -- there is an associated type `Parameters r` which the user
    -- needs to specify. See examples below.
    type Parameters r

    deriveFeature :: Monad m
                  => Parameters r
                  -> Producer (UTCTime, Price) m ()
                  -> Producer (UTCTime, r) m ()

backtestStrategy :: (Feature r, Monad m)
                 => Strategy r
                 -> Parameters r
                 -> Producer (UTCTime, Price)  m ()
                 -> m BacktestResults
backtestStrategy strat params prices
    =   deriveFeature params prices
    >-> Pipes.map (\(k, feature) -> (k, runStrategy strat feature))
    >-> simulateMarketActions

Let’s look at two example instances of Feature. The simplest is the basic feature or Price:

type NoParameters = ()

instance Feature Price where
    -- The `Price` feature has no free parameters
    type Parameters Price = NoParameters

    deriveFeature :: Monad m
                  => NoParameters
                  -> Producer (UTCTime, Price) m ()
                  -> Producer (UTCTime, Price) m ()
    deriveFeatures _ prices = prices

This is easy because there are no parameters. What about looking at the price history?

newtype PriceHistory
    = MkPriceHistory (Series UTCTime Price)

newtype NumTicks
    = MkNumTicks { numTicks :: Int }

instance Feature PriceHistory where
    type Parameters PriceHistory = NumTicks

    deriveFeature :: Monad m
                  => NumTicks
                  -> Producer (UTCTime, Price) m ()
                  -> Producer (UTCTime, PriceHistory) m ()
    deriveFeature (MkPriceHistoryParameters numTicks) prices
        = prices >-> accumulate numTicks
                 >-> Pipes.map (\xs -> (maximum $ Series.index xs, MkPriceHistory xs))
        where
            -- out of scope, see end of blog post for link to source
            accumulate :: Functor m
                       => Int
                       -> Pipe (UTCTime, a) (Series UTCTime a) m ()
            accumulate = (...)

Finally, as an example of the power of this approach, we’ll create a strategy which combines two features.

First, we’ll extend the Feature class to combine two features a and b into one (a, b) feature:

instance (Feature a, Feature b) => Feature (a, b) where

    type Parameters (a, b) = (Parameters a, Parameters b)

    deriveFeature :: Monad m
                  => Parameters (a, b)
                  -> Producer (UTCTime, Price)  m ()
                  -> Producer (UTCTime, (a, b)) m ()
    deriveFeature (paramsA, paramsB) prices
        = Pipes.zipWith (\(k,a) (_, b) -> (k, (a, b)))
                        (deriveFeature paramsA prices)
                        (deriveFeature paramsB prices)

Second, we’ll define a simple strategy that compares the most recent price against the average price of the last 10 ticks:

import Data.Series ( fold, mean )

finalStrategy :: Strategy (PriceHistory, Price)
finalStrategy
    = MkStrategy $ \(MkPriceHistory history, price)
        -> let avgPrice = fold mean history
            in case price `compare` avgPrice of
                GT -> Sell
                LT -> Buy 10
                EQ -> Hold

It is trivial to backtest this strategy like so:

backtestFinalStrategy :: Monad m
                      => Producer (UTCTime, Price) m ()
                      -> m BacktestResults
backtestFinalStrategy = backtestStrategy finalStrategy ( MkNumTicks 10, () )

and voilà!

Conclusion

In this post, I have shown you how to define trading strategies with typed feature parametrization, which is a neat use of type families. It takes advantage of the Haskell type system for type safety AND extensibility to easily create new features.

All code is available in this Haskell module.