When one temperature is not enough: the two-temperature model

Posted on 2019-04-03. Last updated on 2021-12-14.

Estimated reading time of 8 min.

e-mail GitHub LinkedIn ResearchGate OrcID Google Scholar

Temperature is a measure of the average kinetic energy of all particles in a system. An example of such as system is presented below:

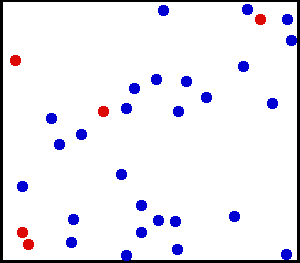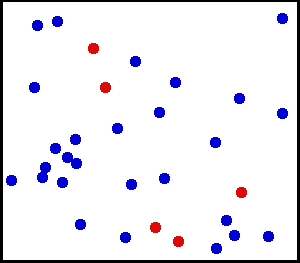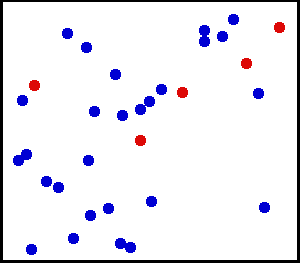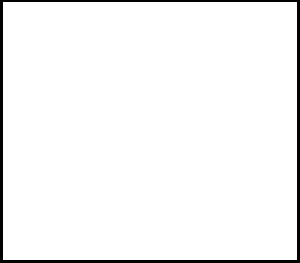
Translational motion of particles in a box. Some particles are colored red for better tracking. Image credit to A. Greg.

Note that the above system has a temperature because there exists a clear average motion, even though not all particles are moving at the same velocity. This means, a system is at some temperature TT as long as the distribution of kinetic energies (often related to velocities) ressembles a normal distribution:

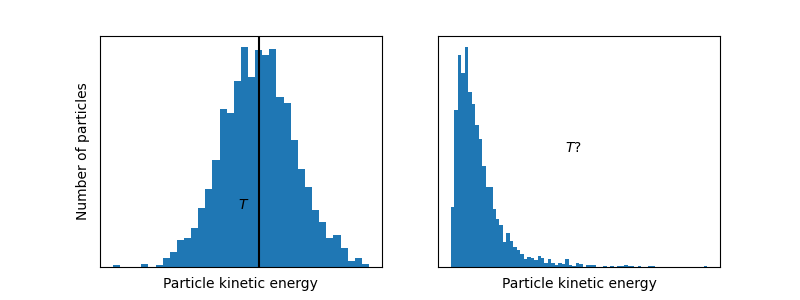
Examples of distribution of particle kinetic energies. Left: distribution of particle energies with a well-defined temperature. Right: distribution of particle energies does not match an expected thermal equilibrium. (Source code)

So, a system with a well-defined temperature exhibits a normal distribution of particle energies. It turns out that it is possible to prepare systems into a state where there are two clear average energies , if only for a very short moment.

Real materials are composed of two types of particles, nuclei and electrons1. These particles have widly different masses, so electromagnetic fields — for example, an intense pulse of light — will not affect them at the same time; since nuclei are at least ~1000x more massive than electrons, we should expect the electrons to react about ~1000x faster.

After decades of development culminating in the 2018 Nobel Prize in Physics, the production of ultrafast laser pulses (less than 30 femtoseconds2) is now routine. These ultrafast laser pulses can be used to prepare systems in a strange configuration: one with seemingly two temperatures, albeit only for a short time. Modeling of this situation in crystalline material was done decades ago, and the model is known as the two-temperature model3.

Roughly 100fs after dumping a lot of energy into a material, the nuclei might not have reacted yet, and we might have the following energetic landscape:

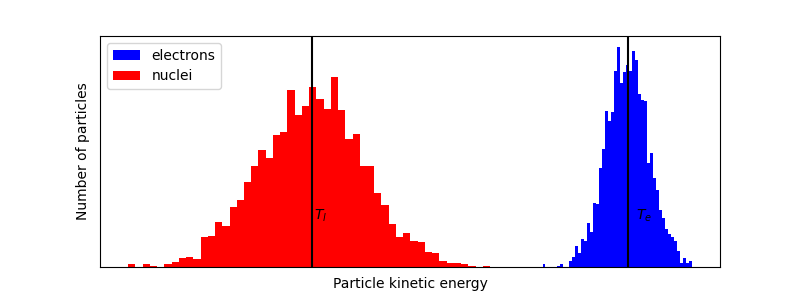
Idealized view of the distribution of kinetic energy, 100 femtosecond after photoexcitation by an ultrafast laser pulse. For a very short time, the system can be described by two temperatures; one for the lattice of nuclei, T_l, and one for the electronic system, T_e. (Source code)

where the nucliei will still be at equilibrium temperature, and the electrons might be at a temperature of 20000∘^{\circ}C. Therefore, we have a system with two temperatures for a few picoseconds4.

  1. The atomic forces at the nanometer-scale are mostly electromagnetic, so I will consider the atomic nuclei as a single particle.↩︎

  2. 11 femtosecond =10−15= 10^{-15} seconds↩︎

  3. P. B. Allen, Theory of thermal relaxation of electrons in metals (1987). Physics Review Letters 59, DOI: 10.1103/PhysRevLett.59.1460↩︎

  4. 11 picosecond =1000= 1000 fs =10−12= 10^{-12} seconds↩︎